Dynamic Programming or DP

Dynamic Programming is a method used in mathematics and computer science to solve complex problems by breaking them down into simpler subproblems. By solving each subproblem only once and storing the results, it avoids redundant computations, leading to more efficient solutions for a wide range of problems. This article provides a detailed exploration of dynamic programming concepts, illustrated with examples.

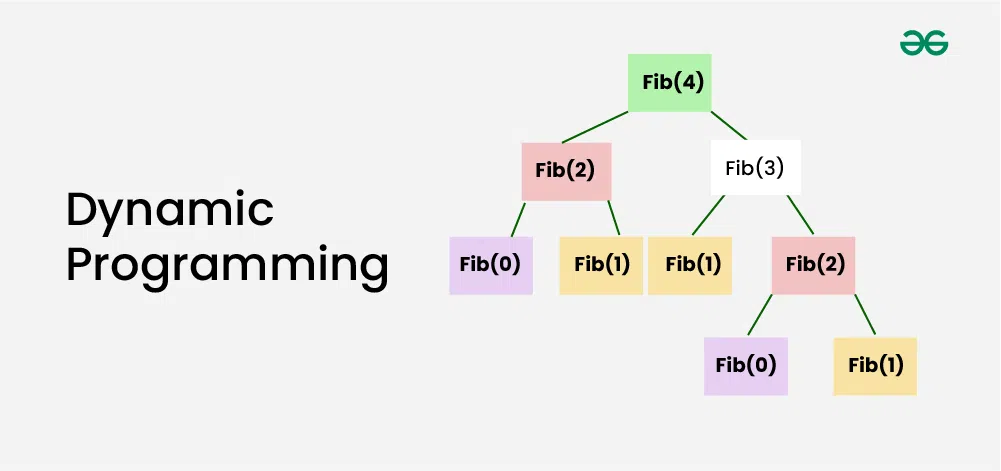
Table of Content

• What is Dynamic Programming ?
• How Does Dynamic Programming Work?
• Examples of Dynamic Programming
• When to Use Dynamic Programming?
• Approaches of Dynamic Programming
• Dynamic Programming Algorithm
• Advantages of Dynamic Programming
• Applications of Dynamic Programming
• Learn Basic of Dynamic Programming
• Advanced Concepts in Dynamic Programming
• Dynamic Programming Problems

What is Dynamic Programming (DP)?

Dynamic Programming (DP) is a method used in mathematics and computer science to solve complex problems by breaking them down into simpler subproblems. By solving each subproblem only once and storing the results, it avoids redundant computations, leading to more efficient solutions for a wide range of problems.

How Does Dynamic Programming (DP) Work?

• Identify Subproblems: Divide the main problem into smaller, independent subproblems.
• Store Solutions: Solve each subproblem and store the solution in a table or array.
• Build Up Solutions: Use the stored solutions to build up the solution to the main problem.
• Avoid Redundancy: By storing solutions, DP ensures that each subproblem is solved only once, reducing computation time.

Examples of Dynamic Programming (DP)

Example 1: Consider the problem of finding the Fibonacci sequence:

Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Brute Force Approach:

To find the nth Fibonacci number using a brute force approach, you would simply add the (n-1)th and (n-2)th Fibonacci numbers. This would work, but it would be inefficient for large values of n , as it would require calculating all the previous Fibonacci numbers.

Dynamic Programming Approach:

Fibonacci Series using Dynamic Programming

• Subproblems: F(0), F(1), F(2), F(3), …
• Store Solutions: Create a table to store the values of F(n) as they are calculated.
• Build Up Solutions: For F(n), look up F(n-1) and F(n-2) in the table and add them.
• Avoid Redundancy: The table ensures that each subproblem (e.g., F(2)) is solved only once.

By using DP, we can efficiently calculate the Fibonacci sequence without having to recompute subproblems.

Example 2: Longest common subsequence (finding the longest subsequence that is common to two strings)

Example 3: Shortest path in a graph (finding the shortest path between two nodes in a graph)

Example 4: Knapsack problem (finding the maximum value of items that can be placed in a knapsack with a given capacity)

When to Use Dynamic Programming (DP)?

Dynamic programming is an optimization technique used when solving problems that consists of the following characteristics:

1. Optimal Substructure:

Optimal substructure means that we combine the optimal results of subproblems to achieve the optimal result of the bigger problem.

Example:

• Find the minimumcost path from the source node to each intermediate node.
• Find the minimumcost path from each intermediate node to the destination node.

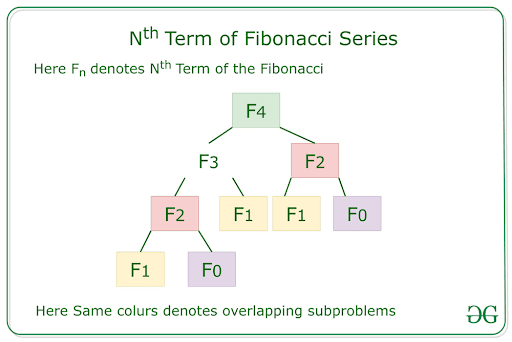
2. Overlapping Subproblems:

The same subproblems are solved repeatedly in different parts of the problem.

Example:

Consider the problem of computing the Fibonacci series . To compute the Fibonacci number at index n , we need to compute the Fibonacci numbers at indices n-1 and n-2 . This means that the subproblem of computing the Fibonacci number at index n-1 is used twice in the solution to the larger problem of computing the Fibonacci number at index n .

Approaches of Dynamic Programming (DP)

Dynamic programming can be achieved using two approaches:

1. Top-Down Approach (Memoization):

In the top-down approach, also known as memoization , we start with the final solution and recursively break it down into smaller subproblems. To avoid redundant calculations, we store the results of solved subproblems in a memoization table.

Let’s breakdown Top down approach:

• Starts with the final solution and recursively breaks it down into smaller subproblems.
• Stores the solutions to subproblems in a table to avoid redundant calculations.
• Suitable when the number of subproblems is large and many of them are reused.

2. Bottom-Up Approach (Tabulation):

In the bottom-up approach, also known as tabulation , we start with the smallest subproblems and gradually build up to the final solution. We store the results of solved subproblems in a table to avoid redundant calculations.

Let’s breakdown Bottom-up approach:

• Starts with the smallest subproblems and gradually builds up to the final solution.
• Fills a table with solutions to subproblems in a bottom-up manner.
• Suitable when the number of subproblems is small and the optimal solution can be directly computed from the solutions to smaller subproblems.

Dynamic Programming (DP) Algorithm

Dynamic programming is a algorithmic technique that solves complex problems by breaking them down into smaller subproblems and storing their solutions for future use. It is particularly effective for problems that contains overlapping subproblems and optimal substructure.

Common Algorithms that Use Dynamic Programming:

• Longest Common Subsequence (LCS): Finds the longest common subsequence between two strings.
• Shortest Path in a Graph: Finds the shortest path between two nodes in a graph.
• Knapsack Problem: Determines the maximum value of items that can be placed in a knapsack with a given capacity.
• Matrix Chain Multiplication: Optimizes the order of matrix multiplication to minimize the number of operations.
• Fibonacci Sequence: Calculates the nth Fibonacci number.

Advantages of Dynamic Programming (DP)

Dynamic programming has a wide range of advantages, including:

• Avoids recomputing the same subproblems multiple times, leading to significant time savings.
• Ensures that the optimal solution is found by considering all possible combinations.
• Breaks down complex problems into smaller, more manageable subproblems.

Applications of Dynamic Programming (DP)

Dynamic programming has a wide range of applications, including:

• Optimization: Knapsack problem, shortest path problem, maximum subarray problem
• Computer Science: Longest common subsequence, edit distance, string matching
• Operations Research: Inventory management, scheduling, resource allocation

Now, let’s explore a comprehensive roadmap to mastering Dynamic Programming.

Learn Basic of Dynamic Programming (DP)

• Introduction to Dynamic Programming – Data Structures and Algorithm Tutorials
• What is memoization? A Complete tutorial
• Tabulation vs Memoizatation
• Optimal Substructure Property
• Overlapping Subproblems Property
• How to solve a Dynamic Programming Problem ?

Advanced Concepts in Dynamic Programming (DP)

• Bitmasking and Dynamic Programming | Set 1
• Bitmasking and Dynamic Programming | Set-2 (TSP)
• Digit DP | Introduction
• Sum over Subsets | Dynamic Programming

Dynamic Programming (DP) Problems

We have classified standard dynamic programming (DP) problems into three categories: Easy, Medium, and Hard.

1. Easy Problems on Dynamic Programming (DP)

• Fibonacci numbers
• nth Catalan Number
• Bell Numbers (Number of ways to Partition a Set)
• Binomial Coefficient
• Coin change problem
• Subset Sum Problem
• Compute nCr % p
• Cutting a Rod
• Painting Fence Algorithm
• Longest Common Subsequence
• Longest Increasing Subsequence
• Longest subsequence such that difference between adjacents is one
• Maximum size square sub-matrix with all 1s
• Min Cost Path
• Minimum number of jumps to reach end
• Longest Common Substring (Space optimized DP solution)
• Count ways to reach the nth stair using step 1, 2 or 3
• Count all possible paths from top left to bottom right of a mXn matrix
• Unique paths in a Grid with Obstacles

2. Medium Problems on Dynamic Programming (DP)

• Floyd Warshall Algorithm
• Bellman–Ford Algorithm
• 0-1 Knapsack Problem
• Printing Items in 0/1 Knapsack
• Unbounded Knapsack (Repetition of items allowed)
• Egg Dropping Puzzle
• Word Break Problem
• Vertex Cover Problem
• Tile Stacking Problem
• Box-Stacking Problem
• Partition Problem
• Travelling Salesman Problem | Set 1 (Naive and Dynamic Programming)
• Longest Palindromic Subsequence
• Longest Common Increasing Subsequence (LCS + LIS)
• Find all distinct subset (or subsequence) sums of an array
• Weighted job scheduling
• Count Derangements (Permutation such that no element appears in its original position)
• Minimum insertions to form a palindrome
• Wildcard Pattern Matching
• Ways to arrange Balls such that adjacent balls are of different types

3. Hard Problems on Dynamic Programming (DP)

• Palindrome Partitioning
• Word Wrap Problem
• The painter’s partition problem
• Program for Bridge and Torch problem
• Matrix Chain Multiplication
• Printing brackets in Matrix Chain Multiplication Problem
• Maximum sum rectangle in a 2D matrix
• Maximum profit by buying and selling a share at most k times
• Minimum cost to sort strings using reversal operations of different costs
• Count of AP (Arithmetic Progression) Subsequences in an array
• Introduction to Dynamic Programming on Trees
• Maximum height of Tree when any Node can be considered as Root
• Longest repeating and non-overlapping substring

Quick Links:

• Learn Data Structure and Algorithms | DSA Tutorial
• Top 20 Dynamic Programming Interview Questions
• ‘Practice Problems’ on Dynamic Programming
• ‘Quiz’ on Dynamic Programming